"Graph coloring deals with the fundamental problem of partitioning a set of objects into classes, according to certain rules... Problems, results and definitions in graph coloring theory have variations, extensions and/or reformulations ad infinitum..."
Bjarne Toft and Tommy R. Jensen, Graph Coloring Problems, Wiley-Interscience 1995
A convenient language that may be used in formulating problems of graph
colouring in a general setting is the language of reducible and decomposable properties of graphs.
Let us denote by 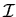 the class of all finite simple graphs. A property of graphs
the class of all finite simple graphs. A property of graphs
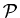 is any nonempty proper isomorphism closed subclass of
is any nonempty proper isomorphism closed subclass of 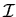 .
Let
.
Let
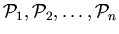 be properties of graphs. A graph
be properties of graphs. A graph 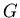 is vertex
is vertex
 -colorable(
-colorable(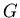 has property
has property
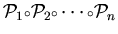 ) if the vertex set
) if the vertex set 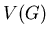 of
of 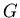 can be partitioned into
can be partitioned into 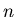 sets
sets
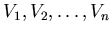 such that the subgraph
such that the subgraph ![$G[V_i]$](img10.gif) of
of 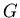 induced by
induced by 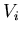 belongs to
belongs to 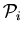 ;
; 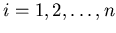 .
In the case
.
In the case
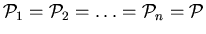 we write
we write
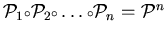 and we say that
and we say that
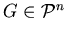 is
is 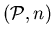 -colorable (partitionable).
Let us denote by
-colorable (partitionable).
Let us denote by 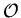 the class of all edgeless graphs. The classical graph coloring problems deals with so-called proper coloring where
the class of all edgeless graphs. The classical graph coloring problems deals with so-called proper coloring where
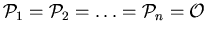 so that a graph
so that a graph 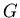 is
is 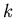 -colorable if and only if
-colorable if and only if
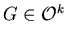 . The basic property of the proper coloring is that every induced subgraph of a
. The basic property of the proper coloring is that every induced subgraph of a 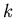 -colorable graph is
-colorable graph is 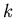 -colorable and if every connected component of a graph
-colorable and if every connected component of a graph 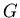 is
is 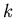 -colorable, then
-colorable, then 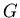 is
is 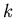 -colorable, too. We consider as the generalizations of the proper coloring only such vertex
-colorable, too. We consider as the generalizations of the proper coloring only such vertex
 -colorings where the properties
-colorings where the properties
 preserve the above mentioned requirements i.e. they are closed to induced subgraphs and disjoint union of graphs. Such properties of graphs are called induced-hereditary and additive. The set of all additive induced-hereditary properties will be denoted by
preserve the above mentioned requirements i.e. they are closed to induced subgraphs and disjoint union of graphs. Such properties of graphs are called induced-hereditary and additive. The set of all additive induced-hereditary properties will be denoted by
![$\mbox{\sf\makebox[0ex][l]{\rule[0ex]{.15ex}{1.55ex}}\makebox[0ex][l]{\rule[1.54ex]{.4ex}{.05ex}}\makebox[.05ex][l]{\rule[0ex]{.4ex}{.05ex}}M}^a$](img22.gif) .
.
Let
![${\cal P}_1,{\cal P}_2,\dots,{\cal P}_n \in \mbox{\sf\makebox[0ex][l]{\rule[0ex]...
...][l]{\rule[1.54ex]{.4ex}{.05ex}}\makebox[.05ex][l]{\rule[0ex]{.4ex}{.05ex}}M}^a$](img23.gif)
, an edge

-
decomposition of
a graph
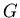
is the decomposition

of its edge set
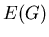
satisfying that for each
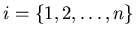
the induced
subgraph
![$G[E_i]$](img27.gif)
has property
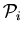
. A property
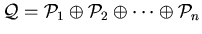
is defined as the set of all graphs having a

-
decomposition.
If
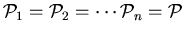
we simply write
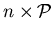
instead of
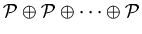
. Note that the property
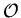
is the neutral element for the operation
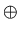
. More precisely, if
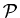
is an induced-hereditary property then
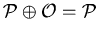
. Let
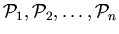
be additive induced-hereditary, then the properties
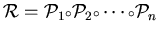
and
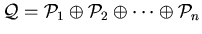
are also additive induced-hereditary.
Reducible and decomposable properties of graphs express a natural generalization of vertex and edge
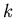
-colorable graphs. The detailed notation, basic results and many examples of induced-hereditary properties may be found in [
1] and [
2] (see also [
3]). The basic results on the cardinality of induced hereditary properties are presented in [
4].
An additive induced-hereditary property
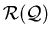
is said to be
reducible (decomposable) if there exist additive induced-hereditary properties
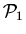
and
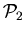
such that

; otherwise the property
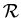
is
irreducible (indecomposable). The notion of reducible property have been introduced in connection with generalized graph colouring and the existence of uniquely partitionable graphs in [
5,
6]. In our three talks we will present a survey of recent results and open problems on reducible and decomposable properties of graphs. Necessary and sufficient conditions for a property to be irreducible will be given. The proof of the Unique Factorization Theorem for additive induced-hereditary properties will be presented.
![]() the class of all finite simple graphs. A property of graphs
the class of all finite simple graphs. A property of graphs
![]() is any nonempty proper isomorphism closed subclass of
is any nonempty proper isomorphism closed subclass of ![]() .
Let
.
Let
![]() be properties of graphs. A graph
be properties of graphs. A graph ![]() is vertex
is vertex
![]() -colorable(
-colorable(![]() has property
has property
![]() ) if the vertex set
) if the vertex set ![]() of
of ![]() can be partitioned into
can be partitioned into ![]() sets
sets
![]() such that the subgraph
such that the subgraph ![]() of
of ![]() induced by
induced by ![]() belongs to
belongs to ![]() ;
; ![]() .
In the case
.
In the case
![]() we write
we write
![]() and we say that
and we say that
![]() is
is ![]() -colorable (partitionable).
Let us denote by
-colorable (partitionable).
Let us denote by ![]() the class of all edgeless graphs. The classical graph coloring problems deals with so-called proper coloring where
the class of all edgeless graphs. The classical graph coloring problems deals with so-called proper coloring where
![]() so that a graph
so that a graph ![]() is
is ![]() -colorable if and only if
-colorable if and only if
![]() . The basic property of the proper coloring is that every induced subgraph of a
. The basic property of the proper coloring is that every induced subgraph of a ![]() -colorable graph is
-colorable graph is ![]() -colorable and if every connected component of a graph
-colorable and if every connected component of a graph ![]() is
is ![]() -colorable, then
-colorable, then ![]() is
is ![]() -colorable, too. We consider as the generalizations of the proper coloring only such vertex
-colorable, too. We consider as the generalizations of the proper coloring only such vertex
![]() -colorings where the properties
-colorings where the properties
![]() preserve the above mentioned requirements i.e. they are closed to induced subgraphs and disjoint union of graphs. Such properties of graphs are called induced-hereditary and additive. The set of all additive induced-hereditary properties will be denoted by
preserve the above mentioned requirements i.e. they are closed to induced subgraphs and disjoint union of graphs. Such properties of graphs are called induced-hereditary and additive. The set of all additive induced-hereditary properties will be denoted by
![]() .
.