Let 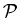 be a property of graphs. A vertex
be a property of graphs. A vertex 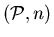 -partition
of a graph -partition
of a graph 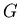 is a partition
is a partition 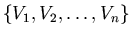 of its vertex set
of its vertex set 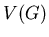 into
into 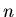 classes such that each
classes such that each 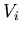 induces a subgraph
induces a subgraph ![$G[V_i]$](img10.gif) with property
with property 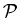 .
A graph .
A graph 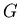 is said to be uniquely
is said to be uniquely 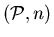 -partitionable, -partitionable, 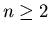 ,
if ,
if 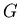 has exactly one
has exactly one 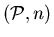 -partition.
In this talk we present a survey on the existence of uniquely partitionable
graphs with respect to induced hereditary properties. Given an additive
induced hereditary property -partition.
In this talk we present a survey on the existence of uniquely partitionable
graphs with respect to induced hereditary properties. Given an additive
induced hereditary property  ,
we prove that uniquely ,
we prove that uniquely  -partitionable
graphs exist if and only if the property -partitionable
graphs exist if and only if the property 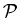 is irreducible. In particular, this implies that for every induced hereditary
property with finitely many connected minimal forbidden induced subgraphs
there are uniquely partitionable graphs.
is irreducible. In particular, this implies that for every induced hereditary
property with finitely many connected minimal forbidden induced subgraphs
there are uniquely partitionable graphs. |
|
 Peter MIHÓK
Peter MIHÓK
Peter MIHÓK