 Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
Zakładu Matematyki Dyskretnej
Wydziału Matematyki Stosowanej
AGH
We wtorek, 18 grudnia 2001 roku, o godzinie 12:45
w sali 304, łącznik A-3-A-4, A G H
Irmina ZIOŁO
(WMS, AGH)
wygłosi referat pod tytułem:
O zanurzaniu digrafów
w swoje dopełnienie
Wiadomo, że graf rzędu 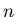 (niezorientowany), mający nie
więcej niż (niezorientowany), mający nie
więcej niż 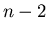 krawędzie może być zanurzony w swoje
dopełnienie. Znanych jest także wiele wyników polepszających
to twierdzenie w różnych kierunkach.
Sytuacja zmienia się dramatycznie, jeśli zamiast grafów
rozpatrujemy digrafy. Hipoteza (Benhocine-Wojda) mówiąca,
że digraf mający nie
więcej niż krawędzie może być zanurzony w swoje
dopełnienie. Znanych jest także wiele wyników polepszających
to twierdzenie w różnych kierunkach.
Sytuacja zmienia się dramatycznie, jeśli zamiast grafów
rozpatrujemy digrafy. Hipoteza (Benhocine-Wojda) mówiąca,
że digraf mający nie
więcej niż 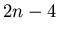 łuki jest zanurzalny, ciągle jest otwarta.
Referat zawiera szkic dowodu pewnego rezultatu dotyczącego
ww. hipotezy. łuki jest zanurzalny, ciągle jest otwarta.
Referat zawiera szkic dowodu pewnego rezultatu dotyczącego
ww. hipotezy.
|
|
| |
Serdecznie zapraszamy wszystkich chętnych !

