Niech 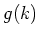 będzie najmniejszą liczbą całkowitą, dla której każdezorientowane drzewo o będzie najmniejszą liczbą całkowitą, dla której każdezorientowane drzewo o 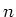 wierzchołkach i wierzchołkach i 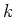 liściach zawiera się w każdymturnieju rzędu liściach zawiera się w każdymturnieju rzędu 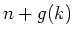 . Na początku lat 90-tych Häggkvist i Thomasondowiedli, że . Na początku lat 90-tych Häggkvist i Thomasondowiedli, że
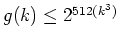 . W czasie referatu będziemyzajmowali się problemem zawierania się w turniejach specjalnego rodzajudrzew zorientowanych. Pokażemy w szczególności, że w każdym turniejurzędu . W czasie referatu będziemyzajmowali się problemem zawierania się w turniejach specjalnego rodzajudrzew zorientowanych. Pokażemy w szczególności, że w każdym turniejurzędu 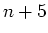 zawiera się dowolne zorientowane drzewo o zawiera się dowolne zorientowane drzewo o 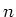 wierzchołkach i 3liściach, co oznacza, że wierzchołkach i 3liściach, co oznacza, że 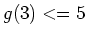 . (!) Jest to wynik Havety z roku 2002.Pokażemy także, że dowolny turniej rzędu . (!) Jest to wynik Havety z roku 2002.Pokażemy także, że dowolny turniej rzędu 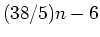 zawiera każdezorientowane drzewo rzędu zawiera każdezorientowane drzewo rzędu 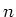 . . |
|